This page is reserved for the description of old cryptographic algorithms, used in cryptographic appliances from the last two decades of the 20th century. They were possibly designed earlier, but used in equipment that was marketed and sold by Philips Usfa and its successor Philips Crypto.
The algorithm of the UA-8295 and UA-8296
Both devices were designed by NOKIA from Finland and equiped with the DES algorithm. See the descriptions at the online Cryptomuseum. Philips replaced the algorithms by more government friendly versions. In both devices the algorithm was programmed in embedded software stored in EPROM’s, so easy to readout, modify and replace. The two scans below are from the original description.
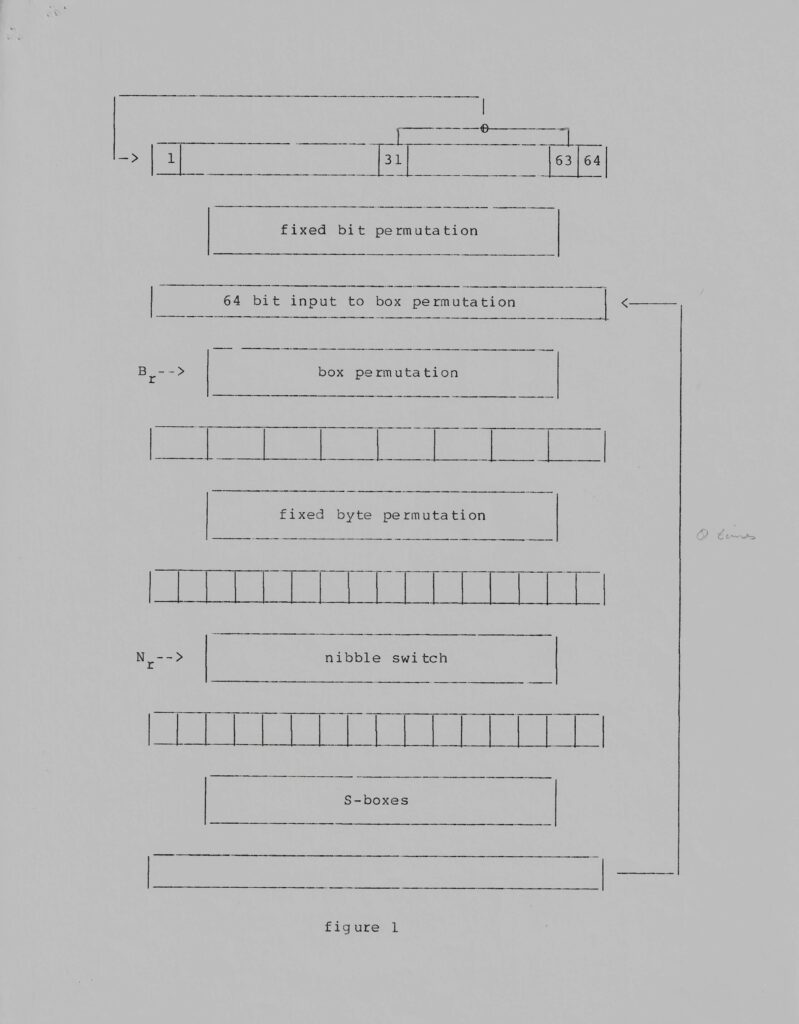

Some time ago, the cryptomuseum acquired a UA-8295. The EPROM’s were read and revealed the structure and details of the cryptographic algorithm, called SBT algorithm, that replaced the DES algorithm in the original Nokia devices. If you are interested in the details of the algorithm, please visit the nice site of the cryptomuseum here.
Meanwhile, I tediously went through old archives and located a couple of programs that were used to calculate some statistics of the SBT algorithm. In those days -the mid 1980’s- Fortran 77 was the programming language and all the guys at Philips were using one computer on a timesharing basis. The computer was a DEC VAX750, also known as miniVax, with a large Winchester hard disk of 80 megabytes. Below is the listing of the program that calculates bit probabilities given some input vector of the algorithm. Implicitly, the program shows the details of the SBT algorithm.
C Programme to determine the output probabilities of 8 RANKS of
C the SBT algorithm.
C Keybits are i.i.d. random variables.
INTEGER*2 NI(16), NB(0:3,16), MDB,LDB, I,J,K,L,M,N, NML,IDN(0:15)
INTEGER*2 BYTP(16), SBOX(0:15,16)
REAL*8 PR(16,0:15), PRI(0:15), PRP(16,0:15)
DATA IDN /0,1,2,3,1,2,3,0,2,3,0,1,3,0,1,2/ ! mod 4 sum, row & column
! Neighbors for 'up', 'left', 'down' and 'right'.
DATA NB /9,3,5,2, 10,4,6,1, 11,1,7,4, 12,2,8,3, 13,7,1,6,
& 14,8,2,5, 15,5,3,8, 16,6,4,7, 1,11,13,10, 2,12,14,9, 3,9,15,12,
& 4,10,16,11, 5,15,9,14, 6,16,10,13, 7,13,11,16, 8,14,12,15/
! Byte Permutation Table (in nibble form)
DATA BYTP /11,12,5,6,15,16,1,2,7,8,3,4,9,10,13,14/
! S - Boxes
DATA SBOX /1,5,4,6,12,10,9,15,3,14,8,0,13,7,2,11, 8,13,7,14,5,0,
&11,10,2,3,12,1,15,4,9,6, 5,2,1,4,13,14,0,9,15,11,6,12,3,10,7,8,
& 9,7,6,13,11,15,4,12,0,8,2,14,10,1,3,5, 11,10,14,0,9,13,3,2,6,12,
&15,7,8,5,4,1, 3,14,13,9,1,4,8,6,10,0,11,5,2,15,12,7, 4,9,8,5,0,6,
&10,14,11,2,7,15,1,3,13,12, 7,15,0,12,10,8,1,11,9,13,5,3,14,2,6,4,
& 2,4,5,12,9,11,7,8,15,14,13,10,3,1,0,6, 7,14,6,8,1,3,0,4,5,15,2,
&14,10,12,11,9, 11,7,9,5,10,1,15,6,2,12,4,13,14,8,3,0, 13,2,12,9,
&14,7,3,1,4,8,0,15,6,10,5,11, 1,8,14,10,7,4,9,13,6,3,11,5,15,0,2,
&12, 8,11,3,14,13,10,4,15,9,0,12,6,5,7,1,2, 15,10,8,13,3,0,14,2,
&12,6,9,1,4,11,7,5, 4,15,10,1,11,2,8,0,13,5,6,12,7,3,9,14/
MDB(I) = ISHFT(IAND(I,'C'X),-2)
LDB(I) = IAND(I,3)
NML(I,J) = 4*I+J
WRITE (6,10)
10 FORMAT (/,5X, 'Give input block (16 hex nibbles) : ',$)
READ (5,'(16Z1)') ((NI(I),NI(I+1)),I=15,1,-2)
C Initializing probability vectors.
DO I = 1,16
PR(I,NI(I)) = 1.
END DO
C Box Permutation
DO NRANK = 1,8
WRITE (6,'(//,5X,''RANK: '',I1)') NRANK
DO I = 1,16 ! Nibble numbers
DO J = 0,15 ! Nibble values
IF (PR(I,J) .NE. 0.) THEN
! 'UP' :
IF (MDB(J) .NE. 0) THEN ! No neighbor involved
K = J - 4 ! Row -1
PRI(K) = PRI(K) + PR(I,J) /4.
ELSE
DO M = 0,15 ! All neighbor values
K = MOD (IDN(M)+LDB(J),4)
K = NML(3,K)
PRI(K) = PRI(K) + PR(NB(0,I),M) * PR(I,J) /4.
END DO
END IF
! 'LEFT' :
IF (LDB(J) .NE. 0) THEN ! No neighbor involved
K = J - 1 ! Column -1
PRI(K) = PRI(K) + PR(I,J) /4.
ELSE
DO M = 0,15 ! All neighbor values
K = MOD (IDN(M)+MDB(J),4)
K = NML(K,3)
PRI(K) = PRI(K) + PR(NB(1,I),M) * PR(I,J) /4.
END DO
END IF
! 'DOWN' :
IF (MDB(J) .NE. 3) THEN ! No neighbor involved
K = J + 4 ! Row +1
PRI(K) = PRI(K) + PR(I,J) /4.
ELSE
DO M = 0,15 ! All neighbor values
K = MOD (IDN(M)+LDB(J),4)
PRI(K) = PRI(K) + PR(NB(2,I),M) * PR(I,J) /4.
END DO
END IF
! 'RIGHT' :
IF (LDB(J) .NE. 3) THEN ! No neighbor involved
K = J + 1 ! Column -1
PRI(K) = PRI(K) + PR(I,J) /4.
ELSE
DO M = 0,15 ! All neighbor values
K = MOD (IDN(M)+MDB(J),4)
K = NML(K,0)
PRI(K) = PRI(K) + PR(NB(3,I),M) * PR(I,J) /4.
END DO
END IF
END IF
END DO
WRITE (6,'(/,5X,I2)') I
WRITE (6,20) ((J,PRI(J)),J=0,15)
20 FORMAT (5X,Z1,5X,D15.8)
DO J = 0,15
PR(I,J) = PRI(J) ! Nibble changed effectively
PRI(J) = 0.
END DO
END DO
C Fixed byte permutation
DO I = 1,16
DO J = 0,15
PRP(BYTP(I),J) = PR(I,J)
END DO
END DO ! This is a very inefficient way
C Nibble Switch
DO I = 1,15,2
DO J = 0,15
PR(I,J) = PRP(I,J)/2. + PRP(I+1,J)/2.
PR(I+1,J) = PR(I,J)
END DO
WRITE (6,'(/,5X,I2)') I
WRITE (6,20) ((J,PR(I,J)),J=0,15)
END DO
C S - Boxes
DO I = 1,16
DO J = 0,15
PRI(SBOX(J,I)) = PR(I,J)
END DO
WRITE (6,'(/,5X,I2)') I
WRITE (6,20) ((J,PRI(J)),J=0,15)
DO J = 0,15
PR(I,J) = PRI(J)
PRI(J) = 0.
END DO
END DO
END DO
END
